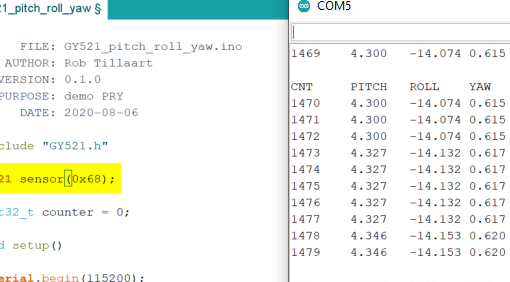
I’m trying to make a simple flight controller for a model rocket, and after some frustration around accelerometers and fin-controlling servos (another post coming on that later) I figured out I could work on a different phase of the flight instead: detecting the apex of the trajectory. To do that I have decided to use a barometric pressure module with my TTGO LoRa32, more specificly the BMP180.

I haven’t got my yet, it is in transit from Germany. So while I wait I will write what I can and hopefully be more or less ready when I get to hook it up to the development board. Since I don’t have it, I will write the code to calculate height from the pressure readings, and a function that detects the apex based on the average of several readings.
The barometric pressure at a given height is very well known and understood, so it’s pretty easy to find a formula and a graph for it. The formula I’m using is
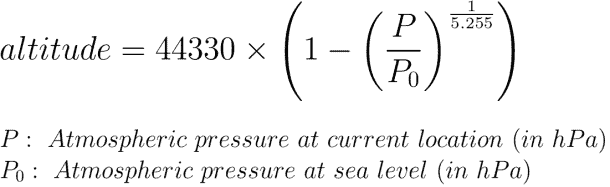
Assuming a P0 at 1013.25 hPa (I will calibrate by reading this at startup when I get the sensor, but this is good enough for now), the same function in python will be
p0 = 1013.25
#function for calculating height from barometric pressure (hPa)
def alt(hPa):
return 44330 * (1-(hPa/p0)**(1/5.255))which for a range of values gives us
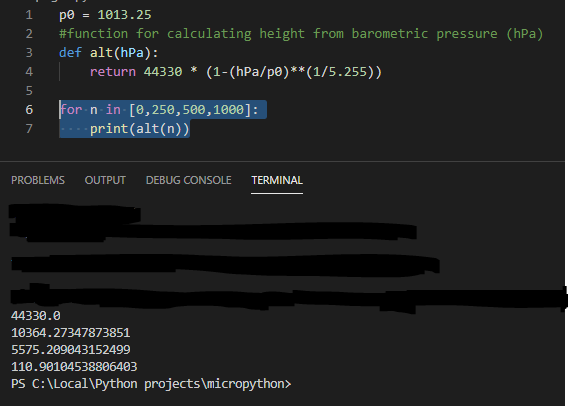
which corresponds pretty good with this chart

Allright! We are now able to determine how high up we are, and can get started on detecting the apex. Roughly speaking, the trajectory is a smooth curve: as long as the altitude is increasing we haven’t reached the apex, and as long as the altitude is decreasing, the apex has been passed. That tells us that we need to compare readings to determine if the current altitude is greater than, equal to or less than the previous altitude. Ok, let’s create a function that tells us which part of the trajectory we’re currently at.
def getTrajectoryStage(lastAltitude, currentAltitude):
if(lastAltitude < currentAltitude):
return "ascending"
if(lastAltitude == currentAltitude):
return "apex"
if(lastAltitude < currentAltitude):
return "descending"Easy peasy lemon sque… wait a minute. Real life called, we have to account for noise during reading and accuracy of the sensor as well! I’m thinking we should use an average of the last three readings. So we get three pressure readings, average them, get the altitude, store it, get three pressure readings, average them, get the altitude and compare it to the last, then keep comparing the altitude of the average of the three past pressure readings to the last until the vehicle is in a passive state (ie. on the ground) again. Since I don’t have a sensor yet, I’ll have to fake the data somehow.
I’m making the easy assumption that the trajectory is shaped like a smooth curve that is evenly distributed on the ascending and descending phase, while in reality there will probably be a quicker ascending rate while under rocket propulsion, then a decreasing ascending rate as the rocket is “free-falling upwards” until it reaches the apex and starts falling towards the ground again.
I figure a decent amount of measurements would be around 15 readings pr second (it’s capable of a lot more, but I’m being cautios for now since I don’t know how much processing power I’m going to need yet) and I’m guessing that the whole flight from launch to landing would take about 15 seconds? That means I have to create 125 measurements. I just divide the amount of required measurements by two and decrease the pressure until I get halfway, or reach apex, and then increase it again until I reach the end, or land. To determine how much to increase by I set a max pressure to reach at 900hPa, which is 988.6 meters, a decent height for a model rocket. I also decided to add noise by choosing a value by random in the range -0.12 to 0.12 hPa and add that to the current value. This helps me write code that probably will work better with the actual values from the sensor. The MBP180 has an accuracy of +-0.12hPa, so this should be good. Here’s how I implemented it in python:
import random
p0 = 1013.25
pMax = 900
#function for calculating height from barometric pressure (hPa)
def alt(hPa):
return 44330 * (1-(hPa/p0)**(1/5.255))
#function for adding noise ()
def addNoise():
noiseRange = range(-12,12,1)
choice = random.choice(noiseRange)
return choice/100 #create decimal range from -0.12 to 0.12
def createFlightPathPressure(nrOfReadings):
readings = []
lastReading = p0 # start at ground level
middle = nrOfReadings // 2
pressureDiff = p0 - pMax
pressureIncrement = pressureDiff / middle
for i in range(0,nrOfReadings,1):
if i < middle:
current = lastReading-pressureIncrement
readings.append(current+addNoise()) #pressure gets lower on the way up
if i >= middle:
current = lastReading+pressureIncrement
readings.append(current+addNoise()) #pressure gets higher on the way down
lastReading = current
return readingsAllright! This gives us the following output:
hpa: 1011.4733870967741, altitude (m): 14.80163586449273
hpa: 1009.6867741935483, altitude (m): 29.707829941324093
hpa: 1007.6501612903224, altitude (m): 46.72591277166945
hpa: 1005.8835483870967, altitude (m): 61.51042823206591
hpa: 1004.1569354838707, altitude (m): 75.98051965697563
hpa: 1002.3903225806449, altitude (m): 90.806702642288
hpa: 1000.513709677419, altitude (m): 106.57924592633084
hpa: 998.6670967741932, altitude (m): 122.1230455525329
hpa: 996.7104838709673, altitude (m): 138.6181800931914
hpa: 995.0238709677415, altitude (m): 152.85814710692006
hpa: 993.1172580645157, altitude (m): 168.9791140929862
hpa: 991.2406451612898, altitude (m): 184.870912523112
hpa: 989.504032258064, altitude (m): 199.59886071153787
hpa: 987.607419354838, altitude (m): 215.7076743100478
hpa: 985.9008064516122, altitude (m): 230.2241542686596
hpa: 983.9841935483864, altitude (m): 246.5511741704629
hpa: 982.1575806451606, altitude (m): 262.13549490466613
hpa: 980.4609677419347, altitude (m): 276.63171635024065
hpa: 978.5943548387088, altitude (m): 292.6039387157892
hpa: 976.787741935483, altitude (m): 308.0862626225589
hpa: 974.8011290322571, altitude (m): 325.1379412253283
hpa: 972.9945161290312, altitude (m): 340.66907389423255
hpa: 971.2279032258054, altitude (m): 355.87893017831937
hpa: 969.4612903225795, altitude (m): 371.11120423165517
hpa: 967.5246774193538, altitude (m): 387.8351151953878
hpa: 965.6880645161278, altitude (m): 403.72052142953993
hpa: 963.971451612902, altitude (m): 418.59014518789087
hpa: 961.9948387096762, altitude (m): 435.7385188779175
hpa: 960.3182258064503, altitude (m): 450.30657948481183
hpa: 958.5016129032244, altitude (m): 466.114361722635
hpa: 956.5049999999986, altitude (m): 483.5164739708832
hpa: 954.8583870967727, altitude (m): 497.8901948937508
hpa: 953.0017741935469, altitude (m): 514.1211542813832
hpa: 951.1251612903211, altitude (m): 530.5529980553663
hpa: 949.3685483870952, altitude (m): 545.95791187972
hpa: 947.5519354838693, altitude (m): 561.9133004818788
hpa: 945.6153225806436, altitude (m): 578.9499538504524
hpa: 943.7987096774177, altitude (m): 594.9566496253696
hpa: 941.9720967741919, altitude (m): 611.0766310296427
hpa: 940.295483870966, altitude (m): 625.8951458258184
hpa: 938.4288709677402, altitude (m): 642.4181395228651
hpa: 936.4422580645142, altitude (m): 660.0326147217847
hpa: 934.6856451612884, altitude (m): 675.6329984111127
hpa: 932.9790322580626, altitude (m): 690.8120870048217
hpa: 930.9324193548367, altitude (m): 709.0449051176527
hpa: 929.1258064516109, altitude (m): 725.1666069142855
hpa: 927.429193548385, altitude (m): 740.3298274532361
hpa: 925.5725806451592, altitude (m): 756.9487831579362
hpa: 923.7759677419333, altitude (m): 773.0563834198837
hpa: 921.9693548387074, altitude (m): 789.2792371915514
hpa: 920.1427419354816, altitude (m): 805.7078748885918
hpa: 918.2161290322558, altitude (m): 823.0645570874384
hpa: 916.53951612903, altitude (m): 838.1930247947685
hpa: 914.522903225804, altitude (m): 856.4191051029437
hpa: 912.8562903225783, altitude (m): 871.5064737801473
hpa: 910.9296774193524, altitude (m): 888.9753673303907
hpa: 909.0730645161266, altitude (m): 905.8378883723849
hpa: 907.3764516129007, altitude (m): 921.2716252820959
hpa: 905.4298387096749, altitude (m): 939.0083719485333
hpa: 903.743225806449, altitude (m): 954.4010873090325
hpa: 901.7266129032231, altitude (m): 972.8360786748403
hpa: 899.9899999999973, altitude (m): 988.7382036168628
hpa: 901.7566129032231, altitude (m): 972.5615873243753
hpa: 903.5732258064489, altitude (m): 955.9538665158714
hpa: 905.3898387096748, altitude (m): 939.373159333591
hpa: 907.3864516129007, altitude (m): 921.1805889185617
hpa: 909.0230645161265, altitude (m): 906.2923943632826
hpa: 910.8496774193524, altitude (m): 889.7013862153283
hpa: 912.7462903225783, altitude (m): 872.5030566272334
hpa: 914.6229032258041, altitude (m): 855.5145419718144
hpa: 916.4795161290299, altitude (m): 838.7348338988716
hpa: 918.1761290322557, altitude (m): 823.4252258308607
hpa: 920.0927419354816, altitude (m): 806.1579482926519
hpa: 921.8493548387074, altitude (m): 790.3577133276448
hpa: 923.6559677419333, altitude (m): 774.1331513316059
hpa: 925.4725806451592, altitude (m): 757.8446712600013
hpa: 927.459193548385, altitude (m): 740.0615120114993
hpa: 929.1058064516109, altitude (m): 725.3452232471748
hpa: 931.0624193548367, altitude (m): 707.8857992725563
hpa: 932.8390322580626, altitude (m): 692.0582833617226
hpa: 934.6456451612885, altitude (m): 675.9885125831543
hpa: 936.4322580645143, altitude (m): 660.1213570914294
hpa: 938.3088709677402, altitude (m): 643.4812726637853
hpa: 940.075483870966, altitude (m): 627.8411733618269
hpa: 942.0720967741918, altitude (m): 610.1934697198186
hpa: 943.9287096774177, altitude (m): 593.8103541003757
hpa: 945.6553225806435, altitude (m): 578.597782669627
hpa: 947.5919354838694, altitude (m): 561.5617122033942
hpa: 949.3685483870952, altitude (m): 545.95791187972
hpa: 951.1151612903211, altitude (m): 530.6406295229052
hpa: 952.9717741935469, altitude (m): 514.3836316643191
hpa: 954.6783870967728, altitude (m): 499.46267927415516
hpa: 956.7149999999987, altitude (m): 481.68476910252144
hpa: 958.3316129032245, altitude (m): 467.59490681885217
hpa: 960.2382258064504, altitude (m): 451.0022127271916
hpa: 961.9948387096762, altitude (m): 435.7385188779175
hpa: 963.9014516129021, altitude (m): 419.1969531862864
hpa: 965.7080645161279, altitude (m): 403.5474038423419
hpa: 967.6446774193537, altitude (m): 386.79804985961715
hpa: 969.3912903225796, altitude (m): 371.7152283058745
hpa: 971.2279032258054, altitude (m): 355.87893017831937
hpa: 973.0645161290313, altitude (m): 340.0668615762928
hpa: 974.7911290322571, altitude (m): 325.22384529201923
hpa: 976.707741935483, altitude (m): 308.7723831060423
hpa: 978.6243548387089, altitude (m): 292.34703991953785
hpa: 980.4209677419346, altitude (m): 276.9737298550467
hpa: 982.0875806451605, altitude (m): 262.73318861237044
hpa: 984.1241935483864, altitude (m): 245.3576870347122
hpa: 985.9208064516123, altitude (m): 230.05391612745444
hpa: 987.5874193548381, altitude (m): 215.8776770060802
hpa: 989.4040322580639, altitude (m): 200.447582509081
hpa: 991.3506451612898, altitude (m): 183.93872315924483
hpa: 993.0972580645157, altitude (m): 169.14835268042017
hpa: 994.9938709677415, altitude (m): 153.11161207934853
hpa: 996.8404838709673, altitude (m): 137.52140834287073
hpa: 998.5170967741932, altitude (m): 123.3866870126954
hpa: 1000.473709677419, altitude (m): 106.91569829443527
hpa: 1002.3203225806449, altitude (m): 91.39460869607855
hpa: 1004.1369354838707, altitude (m): 76.14825010529073
hpa: 1006.0435483870966, altitude (m): 60.170547025503346
hpa: 1007.6601612903224, altitude (m): 46.642284046016854
hpa: 1009.5567741935483, altitude (m): 30.79328836691562
hpa: 1011.3833870967742, altitude (m): 15.552020048086243
hpa: 1013.36, altitude (m): -0.9157606891750114
hpa: 1015.0166129032259, altitude (m): -14.697499613272793Allright, neat! Smashing the numbers into a spreadsheet and hitting the graph button gives this graph:
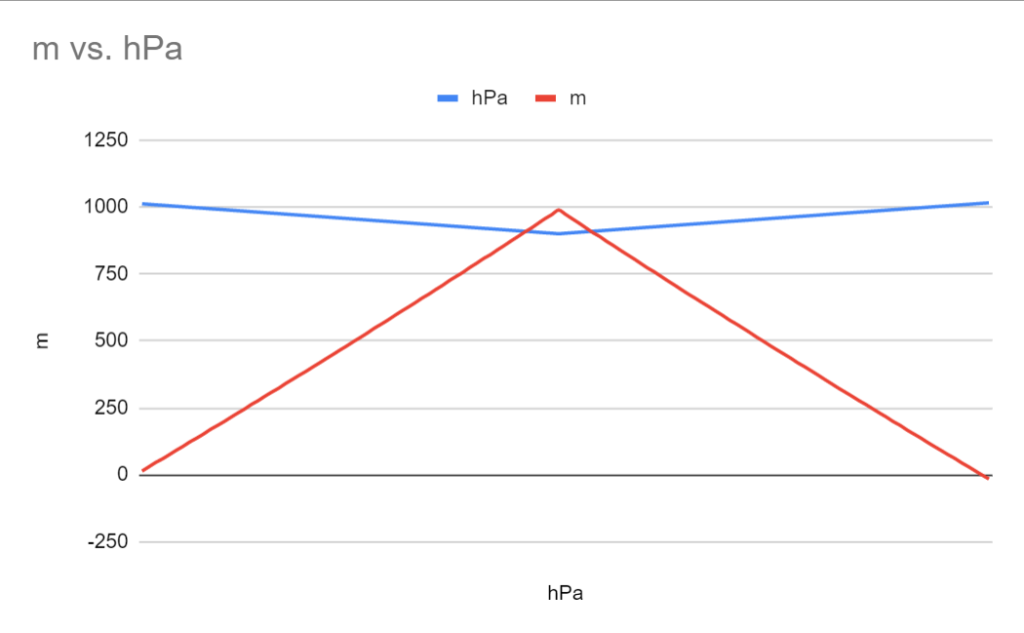
A bit more pointy than I expected, might smooth out the transition from ascending to descending later on. Also, the added noise doesn’t show.. Might be because the scale of the graph isn’t displaying precisely enough. I think I might try a different approach instead… Let’s think about this in terms of high school math! The trajectory is similar to a quadratic function, which we can represent in a vertex form where we already know two of the values: the highest point (on the Y-axis), and the number of steps, or readings, we want to create on the X-axis. Below is the quadratic function in vertex form:
f(x) = a(x-h)^2+kIn this formula, the h stands for where the graph is at its highest point (where the curve changes direction) along the x-axis, and k stands for the highest value along the y-axis. In our case, if we still assume 125 steps, x will be every value between 0 and 125. All that is left then is value a, which tells us how pointy the curve will be, and also in which direction it will be open. To solve for a we need to know two points, and we happen to know three! We want the curve to start at (0,0), we want the curve to have its apex to be at (62,900) which is half of the total steps (yes, I know 62 times 2 is 124…) and the total height we want to reach, and again our curve should reach the x axis (y=0) at (124,0). I changed the number of steps slightly to be able to divide with 2.

Ok, after more googling and trying than I want to admit, here’s my calculation of a for our graph:
vertex: (62,900)
point: (0,0) #we start at 0 readings at 0 altitude
y = a(x-h)^2+k
0 = a(0-62)^2+900
0 = a(-62)^2+900
0 = a * 3844 +900
-900 = a * 3844
-900/3844 = a
-0.2341311134235 ~ a
Our function: f(x) = -0.2341311134235(x-62)^2+900Implementing this is python looks like this
def createTrajectory(maxHeight, nrOfSteps):
a = -0.2341311134235
h = nrOfSteps / 2
k = maxHeight
readings = []
for x in range(0, nrOfSteps, 1):
y = a * ((x - h)**2) + k
readings.append((x,y))
return readings
result = createTrajectory(900,124)Now, you might be thinking this is not precise enough, but it’s close enought for the amount of testing I want to do until my sensor arrives (which should be soon!). The createTrajectory function with the specified input gives us a trajectory that is pretty steep, but I guess that’s how rockets fly anyways… I also came to think that x here is each reading from the sensor, and they will occur at a fixed timing with (hopefully) very little deviation. That means we can calculate the vertical speed of our rocket as well. If we assume that we are able to read the sensor every 100ms, taking calculations and stuff into consideration, we can calculate speed = distance over time like this in python:
def calculateVelocity(distance, ms):
return abs((distance/ms) * 1000) # return speed in m/s as a positive valueI want the function to return it in meters pr second (distance is in meters) and I want the speed to be always positive which is why I use the abs() function. If I didn’t use that I would have gotten a negative velocity as the rocket descends. I guess that would have made it easier to calculate phase? Positive velocity equals ascending, and negative is descending. But instead I tried figuring out a way to calculate the angle of the current point in the trajectory relative to the ground. I know, math again! I had to do some googling again and came across a forum-post somewhere that had a solution I was able to translate into python, but unfortunately I can’t give any credit as I can’t recall where I found it! So whoever you are, dear forum hero person, thank you!
Here’s the formula for calculating the angle relative to the ground
def calculateFlightAngle(previousPoint, currentPoint):
(x1, y1) = previousPoint
(x2, y2) = currentPoint
angle = math.atan2(y2 - y1, x2 - x1) * 180 / math.pi;
return angleIf anyone would care to explain why this works, I would love to hear it. The parts I have figured out so far is that atan2 of the difference between point one and two gives us a vector in radians relative to a horizontal line (the ground), and that the following “* 180 / pi” translates that into degrees. Anyways, this works great, and now we have two inputs we can use to determine flight phase: vertical velocity and angle of the trajectory!
Again, just changing slighty the basic approach from earlier we can assume apex when angle is below a given threshold (on both negative and positive side), and vertical velocity at the same time is below a given threshold. Then, the ascending phase will be when the vertical velocity is above the velocity threshold and the angle is positive and above the angle threshold, while the descending phase is the same, but angle below negative velocity threshold. Here’s how I implemented it
def detectFlightPhase(angle, velocity):
angleTolerance = 15 #degrees
speedTolerance = 3 #meters pr second
if angle > angleTolerance and velocity > speedTolerance:
return "ascending"
if angle < angleTolerance * -1 and velocity > speedTolerance: # negative angle when descending
return "descending"
if angle < angleTolerance and angle > angleTolerance * -1 and velocity < speedTolerance:
return "apex"The tolerance values are selected based on what values I got in the middle of the trajectory so that at least a few values for x would be within the apex. I think they are way to high for a real rocket, but for a proof of concept I guess they’re fine. I actually had to fiddle around a bit to get the trajectory code to work, and since I can’t be on my computer all the time I started using Pydroid3 which works great for stuff like this! Have a look at this short post I wrote about it: Python on Android with pydroid 3
Putting it all together with pretty printing and everything the complete code looks like this
import math
import random
import queue
p0 = 1013.25
pMax = 900
#function for calculating height from barometric pressure (hPa)
def alt(hPa):
return 44330 * (1-(hPa/p0)**(1/5.255))
def addNoise():
noiseRange = range(-12,12,1)
choice = random.choice(noiseRange)
return choice/100 #create decimal range from -0.12 to 0.12
def getTrajectoryStage(altList):
last = altList[0]
for n in altList:
if lastAltitude < currentAltitude:
return "ascending"
if lastAltitude == currentAltitude:
return "apex"
if lastAltitude > currentAltitude:
return "descending"
def createTrajectory(maxHeight, nrOfSteps):
a = -0.2341
h = nrOfSteps / 2
k = maxHeight
readings = []
for x in range(0, nrOfSteps, 1):
y = a * ((x - h)**2) + k
readings.append((x,y))
return readings
def calculateFlightAngle(previousPoint, currentPoint):
(x1, y1) = previousPoint
(x2, y2) = currentPoint
angle = math.atan2(y2 - y1, x2 - x1) * 180 / math.pi;
return angle
def calculateVelocity(distance, ms):
return abs((distance/ms) * 1000) # return speed in m/s as a positive value
def detectFlightPhase(angle, velocity):
angleTolerance = 15 #degrees
speedTolerance = 3 #meters pr second
if angle > angleTolerance and velocity > speedTolerance:
return "ascending"
if angle < angleTolerance * -1 and velocity > speedTolerance: # negative angle when descending
return "descending"
if angle < angleTolerance and angle > angleTolerance * -1 and velocity < speedTolerance:
return "apex"
result = createTrajectory(900,126)
previousX = 0
previousY = 0
timeBetweenReadings = 100
dash = '-' * 76
for value in result:
(reading,altitude) = value
if reading == 0: #print headers
print(dash)
print('{:<4s} {:<19s} {:<19s} {:<20s} {:<11}'.format("X","ALTITUDE (M)","ANGLE (DEG)","VELOCITY (M/S)","PHASE"))
print(dash)
else: #print values
angle = calculateFlightAngle((previousX, previousY), (reading, altitude))
velocity = calculateVelocity(altitude - previousY, timeBetweenReadings)
phase = detectFlightPhase(angle, velocity)
print('{:<4s} {:<19s} {:<19s} {:<20s} {:<11}'.format(str(reading),str(altitude),str(angle),str(velocity), str(phase)))
previousX = reading
previousY = altitude
And running the code gives a printout like this
----------------------------------------------------------------------------
X ALTITUDE (M) ANGLE (DEG) VELOCITY (M/S) PHASE
----------------------------------------------------------------------------
1 0.11959999999999127 6.820179371688774 1.1959999999999127 apex
2 28.913900000000012 88.01096879720959 287.9430000000002 ascending
3 57.24000000000001 87.97811931364735 283.26099999999997 ascending
4 85.09789999999998 87.94416704353242 278.5789999999997 ascending
5 112.48760000000004 87.90905553161382 273.8970000000006 ascending
6 139.40909999999997 87.87272440404094 269.21499999999924 ascending
7 165.86239999999998 87.83510902253394 264.53300000000013 ascending
8 191.84749999999997 87.7961401012896 259.8509999999999 ascending
9 217.36440000000005 87.75574328185536 255.16900000000075 ascending
10 242.4131 87.71383866049345 250.4869999999994 ascending
11 266.9936 87.67034026172705 245.8050000000003 ascending
12 291.1059 87.62515545078479 241.12300000000005 ascending
13 314.75 87.57818427651213 236.4409999999998 ascending
14 337.92589999999996 87.52931873496183 231.75899999999956 ascending
15 360.6336 87.4784419422711 227.07700000000045 ascending
16 382.8731 87.42542720352387 222.3950000000002 ascending
17 404.6444 87.37013696202273 217.71299999999997 ascending
18 425.9475 87.31242161067198 213.03099999999972 ascending
19 446.7824 87.25211814390603 208.34900000000005 ascending
20 467.1491 87.18904862465587 203.6669999999998 ascending
21 487.0476 87.12301843608061 198.98500000000013 ascending
22 506.4779 87.05381428199543 194.30299999999988 ascending
23 525.44 86.98120189285875 189.62100000000078 ascending
24 543.9339 86.90492338551408 184.9389999999994 ascending
25 561.9596 86.82469421420804 180.2570000000003 ascending
26 579.5171 86.74019963719451 175.57500000000005 ascending
27 596.6064 86.65109060680172 170.8929999999998 ascending
28 613.2275 86.55697897028016 166.21099999999956 ascending
29 629.3804 86.45743184289329 161.52900000000045 ascending
30 645.0651 86.35196498199089 156.8470000000002 ascending
31 660.2816 86.24003494913934 152.16499999999996 ascending
32 675.0299 86.12102979397275 147.48299999999972 ascending
33 689.31 85.99425792448716 142.80099999999948 ascending
34 703.1219 85.85893473884637 138.11900000000037 ascending
35 716.4656 85.71416647626805 133.43700000000013 ascending
36 729.3411 85.55893058927718 128.75499999999988 ascending
37 741.7484 85.39205173258632 124.07299999999964 ascending
38 753.6875 85.2121721852426 119.39100000000053 ascending
39 765.1584 85.01771514393768 114.70900000000029 ascending
40 776.1611 84.80683880499954 110.02700000000004 ascending
41 786.6956 84.57737842936282 105.3449999999998 ascending
42 796.7619 84.32677256726195 100.66299999999956 ascending
43 806.36 84.05196816865899 95.98100000000045 ascending
44 815.4899 83.7492972073994 91.2990000000002 ascending
45 824.1516 83.41431436584993 86.61699999999996 ascending
46 832.3451 83.04158072526104 81.93499999999972 ascending
47 840.0704 82.62437140923232 77.25299999999947 ascending
48 847.3275 82.15427427257053 72.57100000000037 ascending
49 854.1164 81.62062952076032 67.88900000000012 ascending
50 860.4371 81.00973221393565 63.20699999999987 ascending
51 866.2896 80.30367307124884 58.524999999999636 ascending
52 871.6739 79.47861319293902 53.84300000000053 ascending
53 876.59 78.50214709190075 49.161000000000286 ascending
54 881.0379 77.32914966064662 44.47900000000004 ascending
55 885.0176 75.89501029912745 39.7969999999998 ascending
56 888.5291 74.10418189482591 35.114999999999554 ascending
57 891.5724 71.80995903830294 30.433000000000447 ascending
58 894.1475 68.77709433803787 25.751000000000204 ascending
59 896.2544 64.60953564496329 21.06899999999996 ascending
60 897.8931 58.60679549537291 16.386999999999716 ascending
61 899.0636 49.49155079659315 11.704999999999472 ascending
62 899.7659 35.08036781518804 7.023000000000366 ascending
63 900.0 13.175673913342347 2.341000000000122 apex
64 899.7659 -13.175673913342347 2.341000000000122 apex
65 899.0636 -35.08036781518804 7.023000000000366 descending
66 897.8931 -49.49155079659315 11.704999999999472 descending
67 896.2544 -58.60679549537291 16.386999999999716 descending
68 894.1475 -64.60953564496329 21.06899999999996 descending
69 891.5724 -68.77709433803787 25.751000000000204 descending
70 888.5291 -71.80995903830294 30.433000000000447 descending
71 885.0176 -74.10418189482591 35.114999999999554 descending
72 881.0379 -75.89501029912745 39.7969999999998 descending
73 876.59 -77.32914966064662 44.47900000000004 descending
74 871.6739 -78.50214709190075 49.161000000000286 descending
75 866.2896 -79.47861319293902 53.84300000000053 descending
76 860.4371 -80.30367307124884 58.524999999999636 descending
77 854.1164 -81.00973221393565 63.20699999999987 descending
78 847.3275 -81.62062952076032 67.88900000000012 descending
79 840.0704 -82.15427427257053 72.57100000000037 descending
80 832.3451 -82.62437140923232 77.25299999999947 descending
81 824.1516 -83.04158072526104 81.93499999999972 descending
82 815.4899 -83.41431436584993 86.61699999999996 descending
83 806.36 -83.7492972073994 91.2990000000002 descending
84 796.7619 -84.05196816865899 95.98100000000045 descending
85 786.6956 -84.32677256726195 100.66299999999956 descending
86 776.1611 -84.57737842936282 105.3449999999998 descending
87 765.1584 -84.80683880499954 110.02700000000004 descending
88 753.6875 -85.01771514393768 114.70900000000029 descending
89 741.7484 -85.2121721852426 119.39100000000053 descending
90 729.3411 -85.39205173258632 124.07299999999964 descending
91 716.4656 -85.55893058927718 128.75499999999988 descending
92 703.1219 -85.71416647626805 133.43700000000013 descending
93 689.31 -85.85893473884637 138.11900000000037 descending
94 675.0299 -85.99425792448716 142.80099999999948 descending
95 660.2816 -86.12102979397275 147.48299999999972 descending
96 645.0651 -86.24003494913934 152.16499999999996 descending
97 629.3804 -86.35196498199089 156.8470000000002 descending
98 613.2275 -86.45743184289329 161.52900000000045 descending
99 596.6064 -86.55697897028016 166.21099999999956 descending
100 579.5171 -86.65109060680172 170.8929999999998 descending
101 561.9596 -86.74019963719451 175.57500000000005 descending
102 543.9339 -86.82469421420804 180.2570000000003 descending
103 525.44 -86.90492338551408 184.9389999999994 descending
104 506.4779 -86.98120189285875 189.62100000000078 descending
105 487.0476 -87.05381428199543 194.30299999999988 descending
106 467.1491 -87.12301843608061 198.98500000000013 descending
107 446.7824 -87.18904862465587 203.6669999999998 descending
108 425.9475 -87.25211814390603 208.34900000000005 descending
109 404.6444 -87.31242161067198 213.03099999999972 descending
110 382.8731 -87.37013696202273 217.71299999999997 descending
111 360.6336 -87.42542720352387 222.3950000000002 descending
112 337.92589999999996 -87.4784419422711 227.07700000000045 descending
113 314.75 -87.52931873496183 231.75899999999956 descending
114 291.1059 -87.57818427651213 236.4409999999998 descending
115 266.9936 -87.62515545078479 241.12300000000005 descending
116 242.4131 -87.67034026172705 245.8050000000003 descending
117 217.36440000000005 -87.71383866049345 250.4869999999994 descending
118 191.84749999999997 -87.75574328185536 255.16900000000075 descending
119 165.86239999999998 -87.7961401012896 259.8509999999999 descending
120 139.40909999999997 -87.83510902253394 264.53300000000013 descending
121 112.48760000000004 -87.87272440404094 269.21499999999924 descending
122 85.09789999999998 -87.90905553161382 273.8970000000006 descending
123 57.24000000000001 -87.94416704353242 278.5789999999997 descending
124 28.913900000000012 -87.97811931364735 283.26099999999997 descending
125 0.11959999999999127 -88.01096879720959 287.9430000000002 descending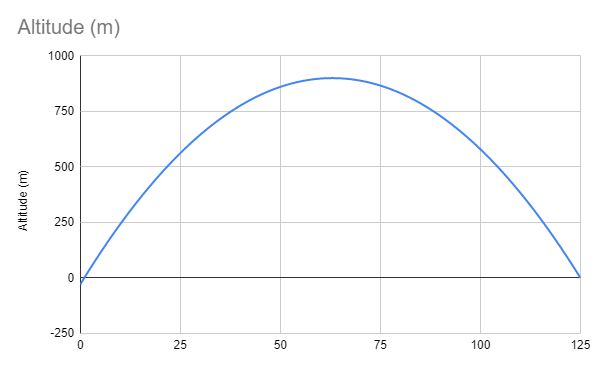
You might have realised I skipped using the noise-generator and the function for calculating altitude from barometric pressure, but since I ended up creating a trajectory in meters I didn’t need it. I will however need it once the BMP180 gets here!
I’m pretty pleased with how this turned out in the end! It’s my first time trying to make anything related to stuff that goes in the air so I might be surprised when I try to run this on an actual device, but I know that I have used some assumptions and estimates here that are likely to be a bit off, and won’t use this on a real rocket on the first go. As soon as I get my sensor I will start implementing this on an ESP32 and write a similar post explaining what I got right and what I got wrong in this post, so stay tuned!